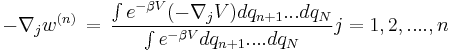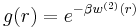Potential of mean force
The Potential of Mean Force [1] of a system with N molecules is strictly the potential that gives the average force over all the configurations of all the n+1...N molecules acting on a particle at any fixed configuration keeping fixed a set of molecules 1...n
For 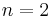 ,
, 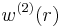 is the average work needed to bring the two particles from infinite separation to a distance
is the average work needed to bring the two particles from infinite separation to a distance  . It is also related to the radial distribution function of the system,
. It is also related to the radial distribution function of the system, 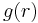 , by[2]:
, by[2]:
Contents |
See also
References
- ^ Kirkwood, J. G. Statistical Mechanics of fluid Mixtures. J. Chem. Phys. 1935, 3, 300; Statistical Mechanics of Liquid Solutions. Chemical Reviews 1936, 19, 275.
- ^ See Chandler, section 7.3
Further reading
- McQuarrie, D. A. Statistical Mechanics.
- Chandler, D. (1987). Introduction to Modern Statistical Mechanics. Oxford University Press.